The Knuth-Plass line breaking algorithm is one of the cornerstones of TeX and why its output looks so pleasing to read (even to people who do not like the look of Computer Modern). While most text editors do line breaking with a quick & dirty algorithm that looks at each line in isolation, TeX does something fancier called minimum raggedness. The basic algorithm defines a global metric over the entire chapter and then chooses line breaks that minimize it. The basic function is the following:
For each line measure the difference between the desired width and the actual width and square the value. Then add these values together.
As you can easily tell, line breaks made at the beginning of the chapter affect the potential line breaks you can do later. Sometimes it is worth it to make a locally non-optimal choice at the beginning to get a better line break possibility much later. Evaluating a global metric like this can be potentially slow, which is why interactive programs like LibreOffice do not use this method.
The classical way of solving this problem is to use dynamic programming. It has the requirement that the problem must conform to a requirement called the Bellman optimality condition (or, if you are into rocketry, the Pontryagin maximum principle). This is perhaps best illustrated with an example: suppose you are in Paris and want to drive to Venice. This requires picking some path to drive that is "optimal" for your requirements. Now suppose we know that Zürich is along the path of this optimal route. The requirement basically says, then, that the optimal route you take from Paris to Zürich does not in any way affect the optimal route from Zürich to Venice. That is, the two paths can be routed independently of each other. This is true for the basic form of Knuth-Plass line breaking.
It is not true for line breaking in practice.
As an example there is an aesthetic requirement that there should not be three or more consecutive lines that end with a hyphen. Suppose you have split the problem in two and that in the top part the last two lines end with a dash and that the first line of the bottom part also ends with a dash. Each of the two parts is optimal in isolation but when combined they'd get the additional penalty of three consecutive hyphens and thus said solution might not be globally optimal.
So then what?
Computers today are a fair bit faster than in the late 70s/early 80s when TeX was developed. The problem size is also fairly small, the average text chapter only contains a few dozen lines (unless you are James Joyce). This leads to the obvious question of "couldn't you just work harder rather than smarter and try all the options?" Sadly the deities of combinatorics say you can't. There are just too many possibilities.
If you are a bit smarter about it, though, you can get most of the way there. For any given point in the raw text there are reasonably only a few places where you could place the optimal line break since every line must be "fairly smooth". The main split point is the one "closest" to the chapter width and then you can try one or two potential split points around it. These choices can be examined recursively fairly easily. So this is what I implemented as a test.
It even worked fairly well for a small sample text and created a good looking set of line breaks in a fraction of a second. Then I tried it with a different sample text that was about twice as long. The program then froze taking 100% CPU and producing no results. Foiled by algorithmic complexity once again!
After a bunch of optimizations what eventually ended up working was to store, for each split point, the N paths with the smallest penalties up to that point. Every time we enter that point the penalty of the current path is evaluated and compared to the list. If the penalty is larger than the worst option then search is abandoned. The resulting algorithm is surprisingly fast and could possibly even be used in real time.
The GUI app
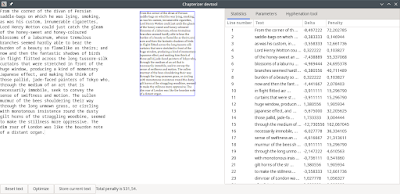
Ideally you'd want to have tests for this functionality. This is tricky, since there is no golden correct answer, only what "looks good". Thus I wrote an application that can be used to examine the behaviour of the program with different texts, fonts and other parameters.
On the left you have the raw editable text, the middle shows how it would get rendered and on the right are the various statistics and parameters to twiddle. If we run the optimization on this piece of text the result looks like this:
For comparison here's what it looks like in LibreOffice:
And in Scribus:
No sample picture of TeX provided because I have neither the patience nor the skills to find out how to make it use Gentium.
While the parameters are not exactly the same in all three cases, we can clearly see that the new implementation produces more uniform results than the existing ones. One thing to note is that in some cases the new method creates lines that are a bit wider than the target box, where the other two never do. This causes the lines to be squished when justified and it looks really bad if done even a bit too much. The optimization function would probably need to be changed to penalize wide lines more than narrow ones.
The code
Get it here. It uses Gtk 4 and a bunch of related tech so getting it to work on anything else than Linux is probably a challenge.
There are a bunch of optimizations one could do, for example optical margin alignment or stretching individual letters on lines that fall far from the target width.