A quantitative analysis of the Trade Federation's blockade of Naboo

The events of Star Wars Episode I The Phantom Menace are based around a blockade that the Trade Federation holds over the planet Naboo. The details are not explained in the source material but it is assumed that this means that no ship can take off or land on the planet. The blockade is implemented by having a fleet of heavily armed star ships around the planet. What we would like to find out is what sort of an operation this blockade was.

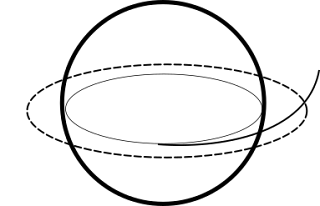
In this analysis we stick only with primary sources, that is, the actual video material. Details on the blockade are sparse. The best data we have is this image.

This is not much to work with, but let's start by estimating how high above the planet the blockade is (assuming that all ships are roughly the same distance from the planet). In order to calculate it from this image we need to know four things

1. The diameter of the planet
2. The observed diamater of the planet on the imaging sensor
3. The physical size of the image sensor 
4. The focal length of the lens

The gravity on Naboo seems to match that of the Earth pretty closely so we'll use an estimate of 6000 km for the planet's radius. Unfortunately we don't know what imaging systems were in use a long time ago in the galaxy far, far away so to get anywhere we have to assume that space aliens use the same imaging technology we have. This gives a reasonable estimate of 35 mm film paired to a 50 mm lens. Captured image width on 35 mm film is 22 mm, so we'll use that value for sensor width. Width is used instead of height to avoid having to deal with possible anamorphic distortions.

Next we need to estimate the planet's observed size on the imaging sensor. This requires some manual curve fitting in Inkscape.

Scaling until the captured image is 22 mm wide tells us that the planet's observed diameter is 30 mm. Plugging these numbers into the relevant equations tells us that the blockade is 2⋅6000⋅50/30 = 20⋅10³ km away from the planet's center. We call this radius r₁. It is established in multiple movies that space ships in Star Wars can take off and land anywhere on a planet. When the queen's ship escapes they have to fight their way through the blockade which would indicate that it covers the entire planet, otherwise they could have avoided the blockade completely just by changing their trajectory to fly through an area where there are no Trade Federation vessels.

How many ships would this require? In order to calculate that we'd need to know how to place an arbitrary number of points on a sphere so that they are all equidistant. There is no formula for that (or at least that is what I was told at school, did not verify) so let's do a lower bound estimate. We'll assume that the blockade ships are at most 10 km apart. If they were any further, the queen's ship would have had no problems flying between the gaps. Each ship thus covers a circular area whose radius is 10 km. We call this r₂. Assuming perfect distribution of blockade vessels we can compute that it takes A₁/A₂ = π⋅(r₁)²/(π⋅(r₂)²) = (r₁)²/(r₂)² = (20⋅10³)²/10² = 4⋅10⁶ or 4 million ships to fully cover the area.

This is not a profitable operation. Even if each ship had a crew complement of only 10, it would still mean having an invasion force of 40 million people just to operate the blockade. There is no way the tax revenue from Naboo (or any adjoining planets, or possibly the entire galaxy) could even begin to cover the costs of this operation.

The equatorial hypothesis

An alternative approach would be that space ships in the Star Wars universe can't launch from anywhere on the planet, only from equatorial sites taking advantage of the boost given by the planet's rotation.

In this case the blockade force would only need to cover a narrow band over the equator. It would need to block it wholly, however, to prevent launches from spaceports all around the planet. Using the numbers above we can calculate that having a ring of ships 10 km apart at blockade height takes approximately 2⋅π⋅r₁/r₂ = 2⋅π⋅20⋅10³/100 = 1300 ships. This is a bit more feasible but not sufficient, because any escaping ship could avoid the blockade by flying 10 km above or below the equatorial plane. Thus the blockade must have height as well and it takes 1300 ships per each 10 km of blockade so a 100 km tall blockade would take 14 000 ships and a 1000 km one would take 130 000 ships. This is better but still not economically feasible.

The alternative planet size hypothesis

In the film Qui-Gon Jinn and Obi-Wan Kenobi are given a submersible called a bongo and told to proceed though the planet's core to get to Theed. The duration of this journey is not given so we have to estimate it somehow. The journey takes place during a military offensive and not much seems to have taken place during it so we assume that it took one hour. Based on visual inspection the bongo seems to travel at around 10 km/h. These measurements imply that Naboo's diameter is in fact only 10 km.

Plugging these numbers in the formulas above tells us that in this case the blockade is at a height of 16 km and would need to guard a surface area of roughly 900 km². The ship count estimation formula breaks down in this case as it says that it only takes 3 ships to cover the entire surface area. In any case this area could be effectively blocked with just a dozen ships or so. This would be feasible and it would explain other things, too.

If Naboo really is this kind of a supermassive mini planet it most likely has some rare and exotic materials on it. Exporting those to other parts of the galaxy would make financial sense and thus taxing them would be highly profitable. This would also explain why the Trade Federation chose to land their invasion force on the opposite side of the planet. It is as far from Theed's defenses as possible. This makes it a good place to stage a ground assault since moving troops to their final destination still only takes at most a few hours.